Defining Aircraft ‘Speed’

Measuring translations and velocities for a ground-based vehicle (your car) is relatively simple as the vehicle is moving with respect to an inertially-fixed reference frame (the Earth), that it is always connected to. To determine how long it will take to get somewhere, distance/time/velocity calculations are simple, and the engine performance is chiefly a function of the vehicle speed.

By comparison, an aircraft is moving with respect to the inertially-fixed reference frame, but it is not connected to it - thus is it difficult to make measurements between the two. Furthermore, aerodynamic performance (how much lift and drag is being produced) is a function of the aircraft’s orientation and translation with respect to the incident wind, and not to the Earth. Similarly, the powerplant performance will be a function of the incident wind and not the groundspeed.

This gives us our first set of ‘speeds’, and the relationship between them:

\[\begin{aligned} V_{gnd} &= V + V_{wind}\label{eq:Vgnd1} \end{aligned}\]

where

\[\begin{split}\begin{aligned} &V_{gnd} : \text{Ground Speed}\nonumber\\ &V : \text{True Airspeed (TAS)}\nonumber\\ &V_{wind} : \text{Wind Speed}\nonumber\end{aligned}\end{split}\]

where we can simply add the two together via vector addition. In the two figures below, the two situations will require the exact same amount of thrust, and the same configuration of control surfaces - but the there is a groundspeed difference of 100kn.

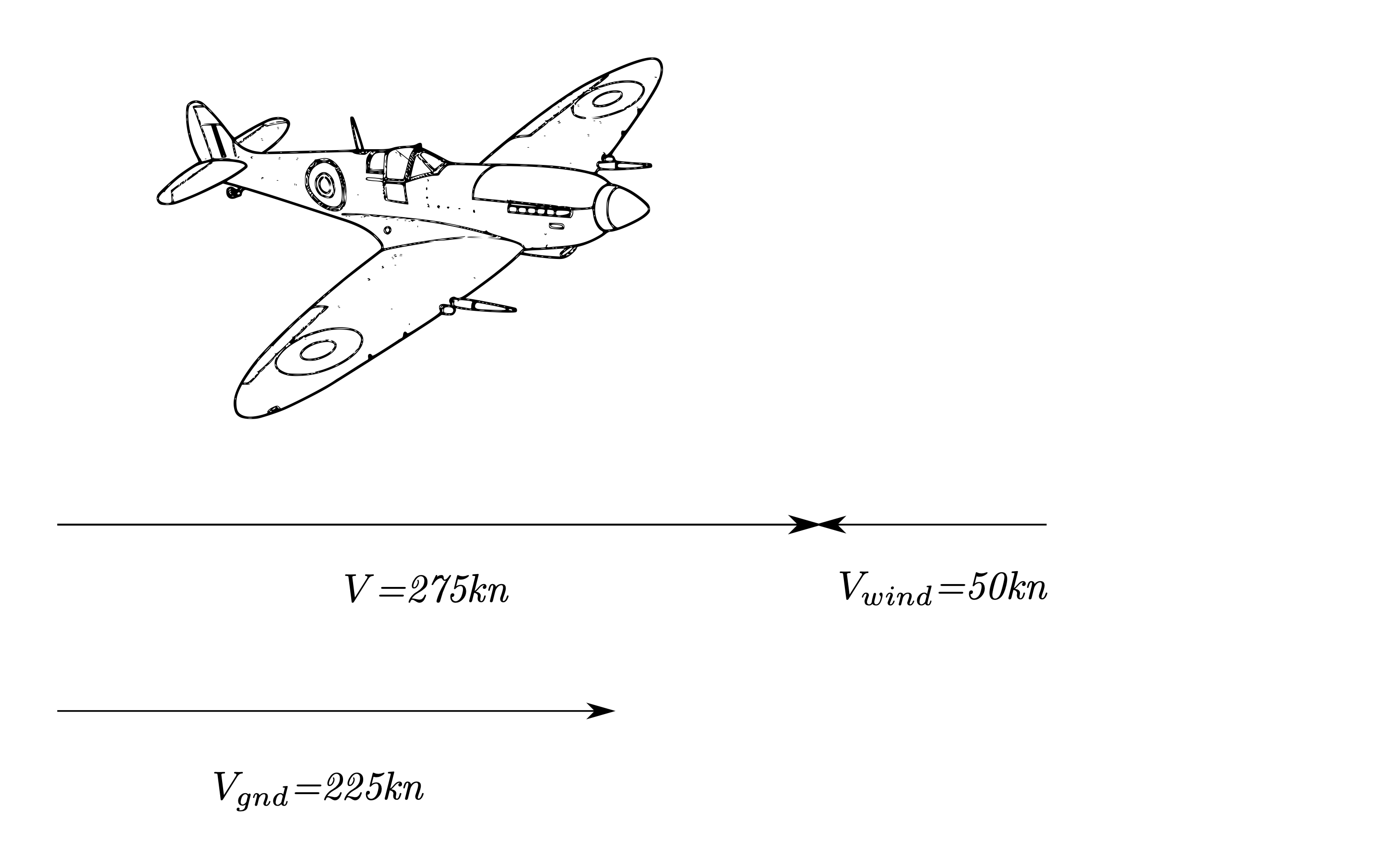
Fig. 14 Aircraft With Headwind

Fig. 15 Aircraft With Tailwind

This is why LHR-ORD takes typically 8h50m, but ORD-LHR takes 7h30m, yet in each case, the aircraft is flying at typical cruise velocity, requiring the same amount of total thrust.

Airspeed Measurement

Clearly aerospace engineers require a means of determining the true airspeed, in order to determine aircraft powerplant/aerodynamic performance, and in order to calculate groundspeed and thus facilitate speed/time calculations.

Equation (1) may be developed from the isentropic flow equations, and allows us to determine true airspeed as a function of density and pressure:

(1)\[V =\sqrt{7\cdot\frac{p}{\rho}\cdot\left\{\left(\frac{\Delta p}{p}+1\right)^\frac{\gamma-1}{\gamma}-1\right\}}\]

where

\[ \begin{align}\begin{aligned}\rho = \text{ Local air density}\\p = \text{ Local static pressure}\\\gamma = \text{ Specific heat ratio = 1.4 for diatomic gases}\\\Delta p = \text{ Dynamic pressure/pressure difference} : p_o-p\\p_o = \text{ Stagnation/total pressure} p_o = \tfrac{1}{2}\rho V^2 + p\end{aligned}\end{align} \]

Equation (1) is often simply given in textbooks with no derivation or explanation. You are encouraged to understand the derivation, but I won’t test you on it.

Click to show the derivation…

This is presented :cite:`Yechout:2014vg`, and other textbooks with no derivation given. It is easily derived from the isentropic flow equations.

The following should be standard from your compressible flow classes, but I want to ensure you understand the legacy of the equations you’re using - so you understand limitations and their development. This is adapted from my own undergraduate notes.

We have the isentropic relationship showing that the ratio of total to static temperature is a function of the Mach number and the ratio of specific heats:

\[ \begin{align}\begin{aligned}\frac{T_{0}}{T}=1+\frac{\gamma-1}{2} M^{2}$$ - (x)\\and we have the isentropic relations\\$$\frac{p_{2}}{p_{1}}=\left(\frac{\rho_{2}}{\rho_{1}}\right)^{\gamma}=\left(\frac{T_{2}}{T_{1}}\right)^{\frac{\gamma}{\gamma-1}}\end{aligned}\end{align} \]

since from total to stagnation we have an isentropic compression of the flow, we can state

\[ \frac{p_{0}}{p}=\left(\frac{\rho_{0}}{\rho}\right)^{\gamma}=\left(\frac{T_{0}}{T}\right)^{\frac{\gamma}{\gamma-1}}\]

the equations above can be combined to give

\[\frac{p_{0}}{p}=\left(1+\frac{\gamma-1}{2} M^{2}\right)^{\frac{\gamma}{\gamma-1}}\label{eq:ISEN1}\]

the fraction may be expressed as:

\[\frac{p_{0}}{p} = \frac{p+\Delta p}{p}=\frac{\frac{p}{p}+\frac{\Delta p}{p}}{\frac{p}{p}}=\frac{\Delta p}{p} + 1\]

where \(\Delta p\) is the \textsl{impact pressure}, and is the difference between total and static in a pitot-static - for incompressible flow, this would be the same as the dynamic pressure, but for compressible flow it is not - hence

\[\frac{\Delta p}{p} + 1=\left(1+\frac{\gamma-1}{2} M^{2}\right)^{\frac{\gamma}{\gamma-1}}\]

\[\frac{2}{\gamma-1}\left[\left(\frac{\Delta p}{p}+1\right)^{\frac{\gamma-1}{\gamma}}-1\right]=M^2=\left(\frac{V}{\sqrt{\gamma\,R\,T}}\right)^2=\frac{V^2}{{\gamma\,R\,T}}\]

\[V^2=\frac{\gamma\,R\,T\cdot 2}{\gamma-1} \left[\left(\frac{\Delta p}{p}+1\right)^{\frac{\gamma-1}{\gamma}}-1\right]\]

from the equation of state, we can express \(R\,T\) as \(\frac{p}{\rho}\)

\[ V^2=\frac{\gamma}{\gamma-1}\cdot\left(\frac{p}{\rho}\right)^2\cdot 2 \left[\left(\frac{\Delta p}{p}+1\right)^{\frac{\gamma-1}{\gamma}}-1\right]\]

the heat capacity ratio, \(\gamma\), is exactly 1.4 for diatomic gases - see footnote - so we can write

\[V = \sqrt{7\cdot\frac{p}{\rho}\left[\left(\frac{\Delta p}{p}+1\right)^{\frac{\gamma-1}{\gamma}}-1\right]}\]

QED

Footnote - Wikipedia isn’t a valid source in most places, but I don’t want to repeat a bit of derivation for an bit of a tangent - https://en.wikipedia.org/wiki/Heat_capacity_ratio#Relation_with_degrees_of_freedom

Equation (1) allows us to determine the velocity with respect to a volume of air, via measurement of three quantities - density \(\rho\), static pressure \(p\), and impact pressure \(\Delta p\). ‘Impact pressure’ is a term that is probably new to you, and refers to the difference between total and static pressure - and, for an incompressible fluid, is the same as dynamic pressure, but not for a compressible fluid.

We have the relationship \(V(p, \rho, \Delta p)\), but the first two quantities are relatively difficult to measure, as they are absolute quantities. Hence, transducers for measurement of absolute pressure and density would require regular calibration, and would add complexity to a measurement system. The reasons for this are complex, and will be elaborated upon in an instrumentation/measurement course - suffice to say that, in general, all transducers are relative transducers, and thus measurement of any absolute quantity require a datum against which they can be compared, calibrated for changes in non-measured quantities, such as temperature.

By contrast, \(\Delta p\) is a relative quantity. Whilst a transducer for measurement will still require calibration, measurement of \(\Delta p\) is relatively easy - for this purpose, we use a pitot-static device. Originally these were analogue devices, measuring the pressure difference between two sides of a pressure chamber via a mechanical diaphragm, calibrated to provide an accurate reading of \(\Delta p\):

Fig. 16 Aircraft Pitot-Static Measurement Device

Calibrated Airspeed

To avoid having to measure \(p\) and \(\rho\), rather than using the pitot-static to measure \(\Delta p\), aircraft Engineers calibrated their devices to provide the correct value of true airspeed at sea-level ISA density and pressure. This provides us with calibrated airspeed, \(V_c\)/CAS, which is only the same as true airspeed at sea-level ISA conditions. \(V_c\) can be calculated via Equation (2):

(2)\[ V_c=\sqrt{7\cdot\frac{p_{SL}}{\rho_{SL}}\cdot\left\{\left(\frac{\Delta p}{p_{SL}}+1\right)^\frac{\gamma-1}{\gamma}-1\right\}}\]

Indicated Airspeed

In reality, such a pitot-static device will measure the calibrated airspeed at a point on the aircraft surface, where the flow has already been disturbed by the aircraft. The device is NOT measuring the freestream velicity - thus there is a position error, based on where the pitot-static is on the aircraft. During flight testing, these inaccuracies can be quantified, and a difference between what is indicated by the device, indicated airspeed/IAS, and calibrated airspeed is determined - \(\Delta V_p\), the position error.

(3)\[V_c = V_I + \Delta V_p\]

At this stage - we have three airspeeds; Indicated (what is shown on the measurement device, for ISA SL conditions), Calibrated (what should be shown on the measurement device, for ISA SL conditions), and True Airspeed. We don’t have a means to convert Calibrated to True yet, so we adopt a two-step approach.

Equivalent Airspeed

The first correction is for the actual pressure at a given altitude. This gives Equivalent Airspeed, EAS.

(4)\[ V_e=\sqrt{7\cdot\frac{p}{\rho_{SL}}\cdot\left\{\left(\frac{\Delta p}{p}+1\right)^\frac{\gamma-1}{\gamma}-1\right\}}\]

where we can see that the sea-level pressure has been replaced with the actual pressure. In practice, this correction is applied as a multiplier between CAS and EAS:

\[V_e = f\cdot V_c\]

where

\[ f = \frac{V_e}{V_c} \]

\[ = \frac{\sqrt{7\cdot\frac{p}{\rho_{SL}}\cdot\left\{\left(\frac{\Delta p}{p}+1\right)^\frac{\gamma-1}{\gamma}-1\right\}}}{\sqrt{7\cdot\frac{p_{SL}}{\rho_{SL}}\cdot\left\{\left(\frac{\Delta p}{p_{SL}}+1\right)^\frac{\gamma-1}{\gamma}-1\right\}}}\]

\[= f(\Delta p, p)\]

Since \(f\) is only dependent on the \(\Delta p\) the aircraft speed, and the \(p\) the aircraft altitude, it can be calculated and tabulated - see the table below for the pressure correction factor:

h, ft		Calibrated Airspeed, kn
	100	125	150	175	200	225	250	275	300
5000	0.999	0.999	0.999	0.998	0.998	0.997	0.997	0.996	0.995
10000	0.999	0.998	0.997	0.996	0.995	0.994	0.992	0.991	0.989
15000	0.998	0.997	0.995	0.994	0.992	0.990	0.987	0.985	0.982
20000	0.997	0.995	0.993	0.990	0.987	0.984	0.981	0.977	0.973
25000	0.995	0.993	0.990	0.986	0.982	0.978	0.973	0.968	0.963
30000	0.993	0.990	0.986	0.981	0.975	0.970	0.963	0.957	0.950
35000	0.991	0.986	0.981	0.974	0.967	0.959	0.951	0.943	0.934
40000	0.988	0.982	0.974	0.966	0.957	0.947	0.937	0.926	0.916
45000	0.984	0.976	0.966	0.956	0.944	0.932	0.920	0.907	0.895
50000	0.979	0.969	0.957	0.944	0.930	0.915	0.901	0.886	0.871

Intermediate values are found via linear interpolation - you should be comfortable with doing this by hand, or by writing code. An example code is provided below that provides two-dimensional interpolation for any values - you can use this function to find out the pressure correction factor - use the syntax f_correction(VC, h) (both of these have default values, so you don’t need to provide either).

import numpy as np
import scipy.interpolate
from scipy.interpolate import interp2d
presscorr = np.array([[5000,0.999,0.999,0.999,0.998,0.998,0.997,0.997,0.996,0.995],
    [10000,0.999,0.998,0.997,0.996,0.995,0.994,0.992,0.991,0.989],
    [15000,0.998,0.997,0.995,0.994,0.992,0.99,0.987,0.985,0.982],
    [20000,0.997,0.995,0.993,0.99,0.987,0.984,0.981,0.977,0.973],
    [25000,0.995,0.993,0.99,0.986,0.982,0.978,0.973,0.968,0.963],
    [30000,0.993,0.99,0.986,0.981,0.975,0.97,0.963,0.957,0.95],
    [35000,0.991,0.986,0.981,0.974,0.967,0.959,0.951,0.943,0.934],
    [40000,0.988,0.982,0.974,0.966,0.957,0.947,0.937,0.926,0.916],
    [45000,0.984,0.976,0.966,0.956,0.944,0.932,0.92,0.907,0.895],
    [50000,0.979,0.969,0.957,0.944,0.93,0.915,0.901,0.886,0.871]])

h = presscorr[:, 0]
VC = np.array([100, 125, 150, 175, 200, 225, 250, 275, 300])
table = presscorr[:, 1:]



f_corr = interp2d(VC, h, table, kind='linear')

def f_correction(VC=125, h=45000, ):
    f = f_corr(VC, h)[0]
    return f

VC = 182
h = 39500
f = f_correction(VC, h)
print(f"For a CAS of {VC}, at an altitude of {h} feet, the pressure correction factor is {f}")

For a CAS of 182, at an altitude of 39500 feet, the pressure correction factor is 0.964336

True Airspeed

Finally, True Airspeed may be calculated from Equivalent Airspeed, by accounting for the actual density at the correct altitude:

\[V = V_e\cdot\sqrt{\frac{\rho_{SL}}{\rho}}\]

\[V = V_e\cdot\sqrt{\frac{1}{\sigma}}\]

\[\sigma = \frac{\rho}{\rho_{SL}}\]

Where we may get the density at different altitudes from standard tables of the atmospheric properties. These are available in the original PDF notes. What we’ll use more regularly is either atmosisa in MATLAB or ambiance in Python.

If you can’t get the following to work - then you might need to install ambiance. Try pip install ambiance in your terminal window. See here for more instructions: https://pypi.org/project/ambiance/

from ambiance import Atmosphere

sealevel = Atmosphere(0)

h = 12000

altmospere = Atmosphere(h)

print(f"At sea level, the pressure is {sealevel.pressure[0]:6.3f}Pa,\
 the density is {sealevel.density[0]:1.3f}kg/m^3,\
 the tempertaure is {sealevel.temperature[0]-273.15:1.1f}C, \
 and the viscosity is {sealevel.kinematic_viscosity[0]:1.3e}kg/s")

print("")

print(f"At an altitude of {h}m, the pressure is {altmospere.pressure[0]:6.3f}Pa,\
the density is {altmospere.density[0]:1.3f}kg/m^3,\
the tempertaure is {altmospere.temperature[0]-273.15:1.1f}C,\
and the viscosity is {altmospere.kinematic_viscosity[0]:1.3e}kg/s")

At sea level, the pressure is 101325.000Pa, the density is 1.225kg/m^3, the tempertaure is 15.0C,  and the viscosity is 1.461e-05kg/s

At an altitude of 12000m, the pressure is 19399.392Pa,the density is 0.312kg/m^3,the tempertaure is -56.5C,and the viscosity is 4.557e-05kg/s

Using ambiance to define the density, we can create a function, sigma_density (it’s a good idea to make function handles descriptive, and there tend to be lots of sigma functions that mean important things in programming languages). This function will return the density ratio for a given altitude provided in metres or feet - bearing in mind than the units for ambiance are metres.

from ambiance import Atmosphere

def sigma_density(h=10000, alt_units='m'):
    if alt_units == 'm':
        factor = 1
    elif alt_units == 'km':
        factor = 1000
    elif alt_units == 'ft':
        factor = 0.3048
    elif alt_units == 'miles':
        factor = 1609.34
    
    sea_level = Atmosphere(0)
    atmospheric_properties = Atmosphere(h*factor)
    
    sigma = atmospheric_properties.density / sea_level.density
    return sigma
    
h_in = 39500

h_unit = 'ft'

print(f"At {h_in}{h_unit}, the density ratio is {sigma_density(h_in, h_unit)[0]:1.6f}")

atm = Atmosphere(39000*.3048)
print(atm.temperature)

At 39500ft, the density ratio is 0.253064
[216.65]

A word about atmospheres

The ambiance module for Python implments the ICAO (International Civial Aviation Organisation) atmopshere, which is an extension of ISA (International Standard Atmosphere).

Printed in the old notes is the US Standard Atmosphere, which is another extension of the ISA model.

Both are equal in the ranges used in this course - but in the printed tables, the values have been truncated. This can lead to differences when interpolating from the table, and when using the routines. See the code dropdown below to understand this further.

# Get four different atmospheres
atmo_sl = Atmosphere(0*.3048)
atmo_35kft = Atmosphere(35000*.3048)
atmo_40kft = Atmosphere(40000*.3048)
atmo_395kft = Atmosphere(39500*.3048)


# Conversions
kg_to_slugs = 1/14.59390
m_to_feet = 3.28084

# Convert the densities
dens_imperial_sl = atmo_sl.density * kg_to_slugs / m_to_feet**3
dens_imperial_35kft = atmo_35kft.density * kg_to_slugs / m_to_feet**3
dens_imperial_40kft = atmo_40kft.density * kg_to_slugs / m_to_feet**3
dens_imperial_395kft = atmo_395kft.density * kg_to_slugs / m_to_feet**3

print(f"The density at 35,000ft from the table is {7.38*1e-4:1.4e}slugs/ft**3 and from ICAO it is {dens_imperial_35kft[0]:1.4e}slugs/ft**3")
print(f"The density at 40,000ft from the table is {5.87*1e-4:1.4e}slugs/ft**3 and from ICAO it is {dens_imperial_40kft[0]:1.4e}slugs/ft**3")
print("")

# Interpolate the densities
dens_interpolated_39500_ambiance = dens_imperial_35kft + 4500/5000 * (dens_imperial_40kft - dens_imperial_35kft)
dens_interpolated_39500_table = 7.38e-4 + 4500/5000 * (5.87e-4 - 7.38e-4)

print(f"The density at 39,500ft from ICAO is {dens_imperial_395kft[0]:1.4e}slugs/ft**3 and interpolated between 35000 and 40000 ICAO it is {dens_interpolated_39500_ambiance[0]:1.4e}slugs/ft**3")

print("")
# Get sigmas
sigma_ambiance_direct = (atmo_395kft.density/atmo_sl.density)[0]
sigma_table = dens_interpolated_39500_table/(23.77*1e-4)
sigma_ambiance = dens_interpolated_39500_ambiance/dens_imperial_sl


print(f"Sigma from the table is {sigma_table:1.4f}, \n from ambiance (at 39000) is is {sigma_ambiance_direct:1.4f}, \n and from ambiance (interpolated between 35000 and 40000) is is {sigma_ambiance[0]:1.4f}")

The density at 35,000ft from the table is 7.3800e-04slugs/ft**3 and from ICAO it is 7.3821e-04slugs/ft**3
The density at 40,000ft from the table is 5.8700e-04slugs/ft**3 and from ICAO it is 5.8728e-04slugs/ft**3

The density at 39,500ft from ICAO is 6.0151e-04slugs/ft**3 and interpolated between 35000 and 40000 ICAO it is 6.0237e-04slugs/ft**3

Sigma from the table is 0.2533, 
 from ambiance (at 39000) is is 0.2531, 
 and from ambiance (interpolated between 35000 and 40000) is is 0.2534

The inputs can also be numpy arrays

alts = np.arange(1, 10)
sigmas = sigma_density(alts, 'miles')

for alt, sigma in zip(alts, sigmas):
    if alt == 1:
        print(f"At an altitude of {alt} mile, the density ratio is {sigma}")
    else:
        print(f"At an altitude of {alt} miles, the density ratio is {sigma}")
         
# Note that the syntax to write mile/miles for single vs. any other quatity is completely unnecessary but nice

At an altitude of 1 mile, the density ratio is 0.8544179176392871
At an altitude of 2 miles, the density ratio is 0.7256946830480345
At an altitude of 3 miles, the density ratio is 0.6124148561281167
At an altitude of 4 miles, the density ratio is 0.5132337621724308
At an altitude of 5 miles, the density ratio is 0.42687647082233393
At an altitude of 6 miles, the density ratio is 0.3521367607463307
At an altitude of 7 miles, the density ratio is 0.28579654351527745
At an altitude of 8 miles, the density ratio is 0.22195323343439954
At an altitude of 9 miles, the density ratio is 0.17239372263976577

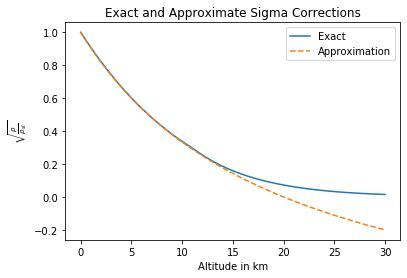
Approximate density correction

For altitudes below about 16km, the approximation can be used

\[\sigma=\frac{20-H}{20+H}\]

where \(H\) is the altitude in \(km\).

The error in this approximation is easily shown using the functions created above:

def sigma_approx(H):
    sigma = (20 - H ) / (20 + H)
    return sigma

Hs = np.linspace(0, 30e3, int(30e3))

sigma_exact = sigma_density(Hs)
sigma_approximation = sigma_approx(Hs/1e3)

import matplotlib.pyplot as plt

plt.figure()
plt.plot(Hs/1e3, sigma_exact, '-', label="Exact")
plt.plot(Hs/1e3, sigma_approximation, '--', label="Approximation")
plt.legend();
plt.title('Exact and Approximate Sigma Corrections')
plt.xlabel('Altitude in km')
plt.ylabel('$\\sqrt{\\frac{\\rho}{\\rho_{sl}}}$');

Why use EAS?

Equivalent airspeed is actually very useful (though pilots tend not to actually use it, annoyingly). We tend to define \(q_\infty\) as \(\tfrac{1}{2}\rho_{SL}V_e^2\), which means that aerodynamic coefficients remain the same for a given \(V_e\) and \(\alpha/\beta\).

It is useful to see that the Equivalent Air Speed (EAS) for a given flight condition, \(V_e\), is the speed which if flown at standard sea level density (\(\rho_{sl} \sim 1.225 kg\cdot m^{-3}\)) would give the same aerodynamic loads, for the same aerodynamic configuration, constant \(C_L\).

This is useful for simplicity of calculations, but is also useful for ease of flight - stall will always occur at the same angle, for the same EAS, regardless of flight altitude. Structural limits are always defined in EAS for the same reason, as the loads are constant at any altitude for the same EAS.

Summary of Corrections

We can remember the order of corrections by the mnemonic “ICE-T”, with the relative magnitudes of the velocities given by the shape that loosely looks like a square root -

Fig. 17 Airspeed Corrections

Problems:

Below are a range of numerical and theoretical questions. Some of the numerical questions have random numbers that change each time the notes get updated - so you’re not going crazy if you thought it was different last time.

Try and go through the questions on your own before looking at the solutions - questions you’ll face in tests/exams will be similar but not exactly the same, so you need to be able to understand the why of the solution rather than just following an algorithm.

Problem 1.1 - Conversion between airspeeds

An aircraft is flying at an altitude of 15000ft, with a calibrated airspeed of 170kn, with a 2kn tailwind:

a) How long will it take to cover 100 miles?

b) How long will it take to cover 200km?

c) If instead of \(V_C\) = 170kn, you have \(V_I\) = 170kn, with a position error of \(\Delta V_P=+2kn\), what do the above answers change to?

Try and tackle the problem yourself before you see the solution below. The numbers in this problem will change each time the notes are updated.

Click to show the solution…

The first step is to take Vc to Ve via the pressure correction.

For the altitude of 15000ft, with a calibrated airspeed of 170kn, the pressure correction can be interpolated from table using the function created earlier with syntax press_correction = f_correction(15000, 170).

This gives a value of 0.994 for the pressure correction, and this determination pf the equivalent airspeed from \(V_e = V_c\cdot f\) so, \(V_e=\)169.014kn.

For EAS to TAS, the density ratio is required - \(\sigma=\frac{\rho}{\rho_{sl}}\), and this is found to be \(\sigma=\)0.629kn. Since this is an altitude above sea level, this has to be a number smaller than one - if it’s not, then you’ve done something wrong.

True airspeed is obtained from the relationship \(V=V_e\cdot\sigma^{-\frac{1}{2}}\) which yields \(V\)=213.029kn.

Note that at no point have the units had to be converted into SI to make the corrections - that’s the smart part of the density and pressure corrections; they are both non-dimensional corrections. If you have velocity in knots, you use them and get velocity in knots out.

Since the wind is a tailwind, this is added to the value above to yield the groundspeed in knots as 215.029kn. This gives the speed of the aircraft relative to the ground, and hence the speed we require for distance/time calculations.

With the velocity in knots it may be easily converted to m/s by multiplying by 0.5144444 which yields \(V\)=110.621m/s.

100 miles is 160,934m, and hence this is covered in 1454.8s or 24 minutes, 14 seconds

200 km is 200,000, and hence this is covered in 1808.0s or 30 minutes, 7 seconds

---

For the last part of the question, this is solved by recalling that \(V_c = V_I + \Delta V_p\) and hence the speeds calculated are now:

\(V_c\) = 172.000kn

\(V_e\) = 170.989kn

\(V\) = 215.518kn

\(V_g\) = 217.518kn = 111.901m/s

The times taken are found to be 23 minutes, 58 seconds and 29 minutes, 47 seconds, for a respective 16 seconds and 20 seconds faster.

Problem 1.2 - Theory

a) When converting between different airspeeds, how can you ‘sense check’ your numbers?

Click to show the solution…

Look at the square-root symbol for ICE-T Airspeed Corrections. This shows the respective magnitude of the velocities you should expect to find.

Once you have the true airspeed, you should also compare it to the type of aircraft listed (if one is). The speed of sound is about 340m/s at sea-level - so if you’ve been given a light commuter aircraft, and you’ve found a true airspeed of 500m/s then something is wrong. (You probably got the knots to metre/s conversion wrong - see here

b) What is the significance of “equivalent airspeed”, and why is it preferable to use when defining limiting speeds for aircraft

Click to show the solution…

For a given angle of attack, the dimensional lift on a given aircraft will be the same for constant \(V_e\) at any altitude. This is not the same for any of the other airspeeds.

Hence - the stall speed (which we will calculate soon) is constant with altitude when defined in EAS, as is the “never exceed” speed (provided \(V_{ne}\) has been defined due to aerodymamic structural limitations.

c) In what cases could you find that your true airspeed is less than your calibrated airspeed?

Click to show the solution…

Flight below sea-level, or if you’ve made a mistake.

d) For what conditions is EAS equivalent to TAS?

Click to show the solution…

Flight at sea-level.