Longitudinal Stability

Through the remainder of the course, means will be developed to analyse the full stability characteristics of aircraft, including the dynamic behaviour. For this, we will separate the aircraft into longitudinal motion (pitching), and combined lateral/directional (rolling/yawing).

For the purposes of static stability, aircraft motion can be isolated to looking at moments about each of the three axes independently.

Longitudinal stability is more interesting and more complicated than than both lateral and directional stability, so it will be analysed first and the same techniques used to explore the other two axes.

For longitudinal stability, the static response is concerned with the aircraft pitching motion - so the parameter of interest is the pitching moment. A model needs to be formulated than can account for the combined effect of the wing, horizontal stabiliser, the elevator, and the aircraft weight therereupon. The pitching moment coefficient is defined

\[C_m\triangleq\frac{M}{\tfrac{1}{2}\rho V^2 S\bar{c}}\]

Before building a model, consider what stability would look like for aircraft pitching motion. The desired behaviour for stability would be that if the aircraft were perturbed in pitch, it would return to the equilibrium position. That is, pitch stability means that a nose-up perturbation is accompanied by a nose-down pitching moment.

Stability Derivatives

The assumption is made that the aircraft pitching moment can be represented as the product of terms comprising the product of stability derivatives and variables, and constants.

The stability derivatives are written in non-dimensional form as:

\[C_{A_B}=\frac{\partial C_A}{B}\]

The pitching moment coefficient is assumed to be of the form:

\[C_m = C_{m_0} + C_{m_\alpha}\cdot\alpha + C_{m_Q}\cdot{Q}\]

where \(C_{m_0}\) is a constant term and hence does not affect stability in any way.

Condition for \(C_{m_\alpha}\)

Since \(\alpha\) is defined as a nose-up motion, and \(M\) is defined positive nose-up, it follows that for stability, \(C_{m_\alpha}\) must be negative

\[\begin{split}\begin{align} C_{m_\alpha} &< 0 \rightarrow\text{stable}\\ C_{m_\alpha} &>0 \rightarrow\text{unstable}\\ \end{align}\end{split}\]

What aircraft design parameters lead to \(C_{m_\alpha}\) being negative? A full model will be formulated that will lead to design parameters, but some simple observations can be made from first principles. Consider the respective longitudinal locations of the aircraft centre of gravity (CG), and the aircaft aerodynamic centre (AC).

Aircraft AC

You will be familiar with centre of pressure and aerodynamic centre from 2D aerofoil theory - the point at which the lift can be assumed to act as a resultant force, and the point at which the moment is independent of AoA, respectively.

The CP moves with angle of attack for a cambered aerofoil, whilst the AC is a fixed position.

There are two possibilties; the AC can be ahead of the CG, or the AC can be behind the CG.

AC Ahead of CG

Fig. 30 AC ahead of CG

Consider the case with the AC ahead of the CG. The lift is directly proportional to the angle of attack, and the nose-up moment is directly proportional to the lift. In the following, \(M_0\) represents the lift independent pitching moment and the pitching moment at \(\alpha=0\) for the sake of mathematical simplicity.

\[M(\alpha) = M_0 + a\cdot\alpha\cdot l\]

\[\frac{\text{d}M}{\text{d}\alpha}= a\cdot l > 0\]

So with the AC ahead of the CG, the aircraft is statically unstable in pitch.

AC Aft of CG

Fig. 31 AC aft of CG

Consider the case with the AC aft of the CG.

\[M(\alpha) = M_0 - a\cdot\alpha\cdot l\]

\[\frac{\text{d}M}{\text{d}\alpha}= -a\cdot l < 0\]

So with the AC aft of the CG, the aircraft is statically stable in pitch.

This shows why most aircraft except fighter aircraft have aft horizontal tails - the horizontal tail pulls the aerodynamic centre aft, and allows the CG to be moved further aft.

A model will be formulated to show the numerical relationship between the tail and the aerodynamic centre, but the result above has been shown from first principles, and is instructive and intuitive. If you’re still not wholly satisfied in this result - try throwing a dart/nerf vortex/arrow “tail first”. It will immediately flip over.

So the stability condition for \(C_{m_\alpha}\) has been established, and a model will be developed to relate design parameters to the numerical value thereof. Before this, though, the stability of \(C_{M_Q}\) will be explored.

Condition for \(C_{m_Q}\)

Using similar reasoning, both conditions for AC/CG location can be overlaid in a single diagram:

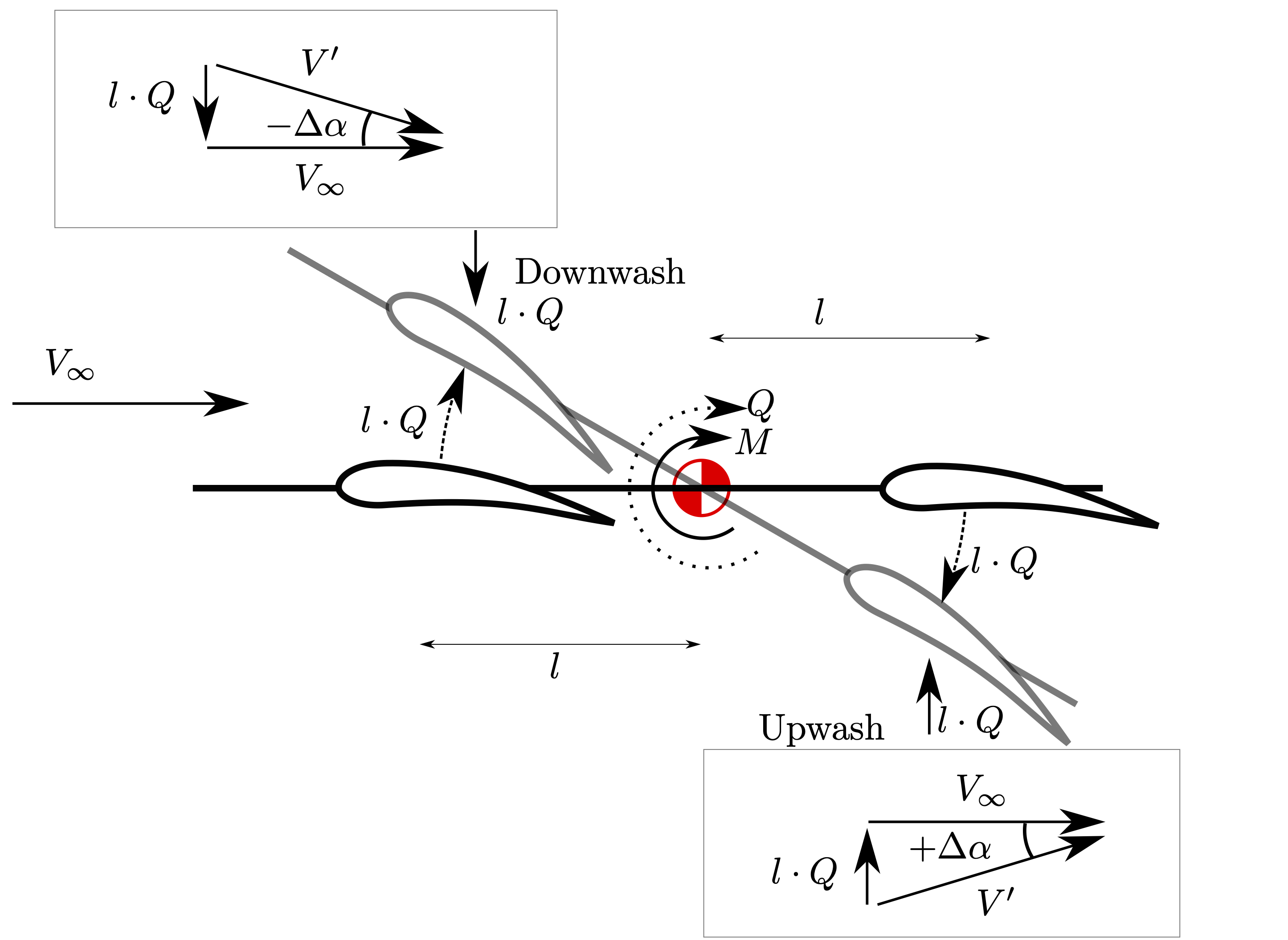
Fig. 32 CP and CG with a pitch rate

Looking at Figure CP and CG with a pitch rate it can be readily seen that a positive pitch rate will cause an downwash for AC ahead of CG, and a upwash for AC aft of CG. This causes a respective decrease and increase in angle of attack, and lift. So for any AC/CG location, the derivative \(C_{M_Q}\) will always be negative and hence restorative.

Second order system representation

The aircraft pitching motion can be modeled as a second order system

Fig. 33 Second order system for pitching motion

This representation should be familiar for you from previous courses, and will be used more in later modules - but for now it serves to help understand the concepts of \(C_{m_\alpha}\) and \(C_{m_Q}\). The former represents the pitch stiffness, whilst the latter represents the pitch damping.

Too much stability?

Whilst it can be readily observed that for stability \(C_{m_\alpha}<0\), with this term now being described as pitch stiffness, you will be able to further observe that it gives an indication of how difficult it is to get an aircraft to move manoeuvred from steady flight. As such, if an aircraft is too stable, its handling is sluggish. Fundamentally, this explains the planform differences between fighter aircraft and commuter aircraft.

A model for pitch stability

A simplified aircraft representation will be used that comprises the aircraft wing, HT, elevator, and centre of gravity:

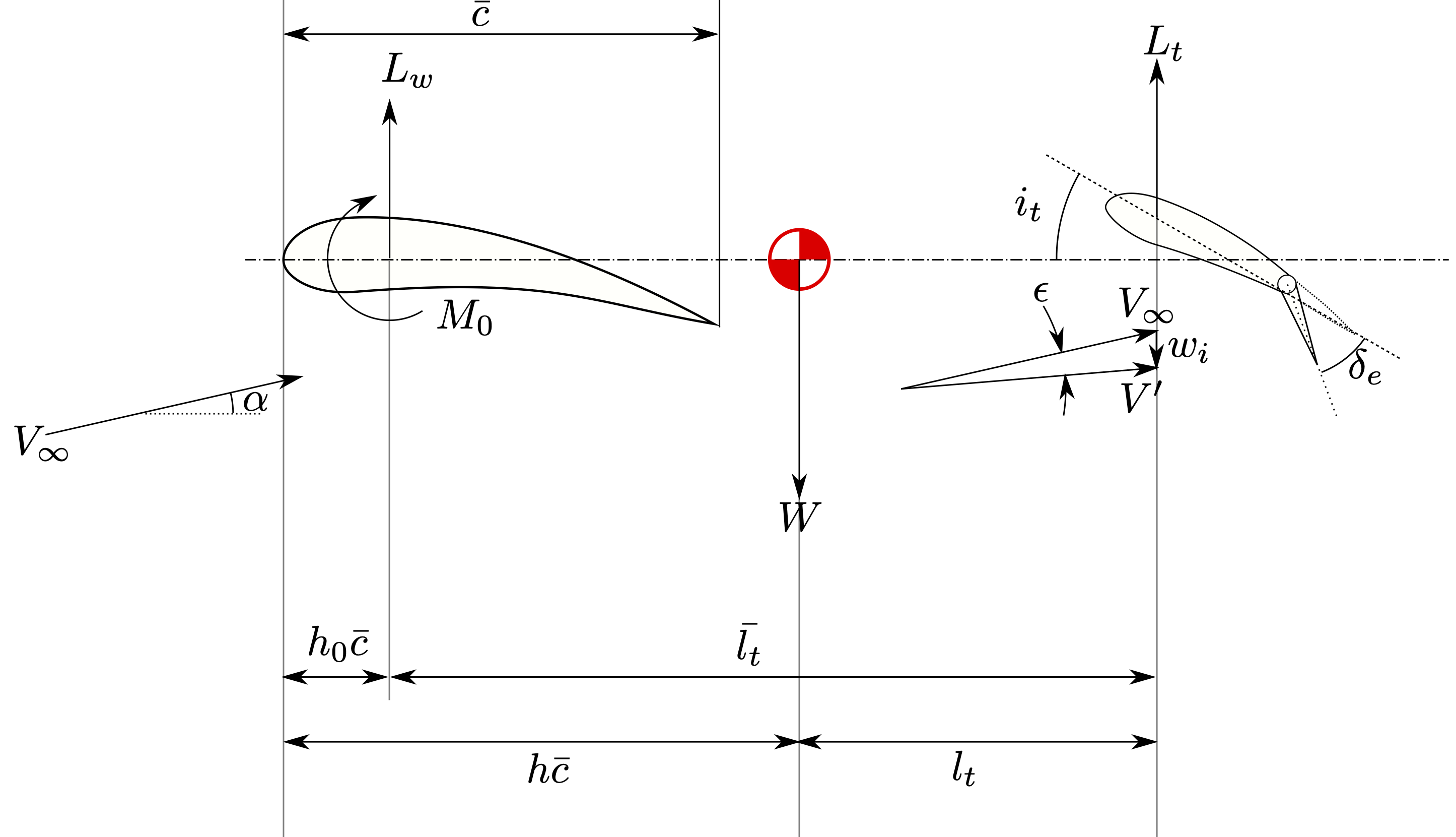
Fig. 34 Model for wing/HT contribution to pitching moment

where

\[\begin{split}\begin{align} \bar{c} &= \text{Mean aerodynamic chord}\\ L_w &= \text{Wing lift}\\ L_t &= \text{Tail lift}\\ M_0 &= \text{Zero lift pitching moment (taken to represent wing/tail combination)}\\ \alpha &= \text{AoA at the main wing}\\ i_t &= \text{Tail incidence}\\ \delta_e &= \text{Elevator deflection angle}\\ w_i &= \text{Downwash due to wing}\\ \epsilon &= \text{Resultant change to incidence at tail due to downwash}\\ V^\prime &= \text{Resultant velocity vector at tail}\\ h_0\bar{c} &= \text{Distance between forward moment ref. point and wing AC}\\ h\bar{c} &= \text{Distance between forward moment ref. point and a/c CG}\\ l_t &= \text{Distance between CG and AC of tail}\\ \bar{l}_t &= \text{Distance between wing AC and tail AC} \end{align}\end{split}\]

Control surface deflections

Some texts use \(\xi\), \(\eta\), and \(\zeta\) for aileron, elevator, and rudder deflections - but who, aside from actual Greeks, can write \(\xi\) and \(\zeta\) consistently distinguishable? Certainly not me.

We’ll use the slightly-more accessible nomenclature of \(\delta_a\), \(\delta_e\), and \(\delta_r\). This is more commonplace in US texts anyway.

Note that the forward moment reference point has been written as the leading edge of the wing, but this is an arbitrary point about which moments are evaluated. It could be the nose, for example.

CP or AC?

To resolve lift as a constant force, it should be applied at the centre of pressure. To decouple the moment from incidence, the lift force should be applied at the aerodynamic centre.

In the analysis herein, the aerofoils are approximated as thin and symmetric which means both the AC and CP can be treated as the quarter chord position.

For a real cambered aerofoil, the CP moves with angle of attack and is at a location infinitely far behind the aerofoil. This obviously makes the analysis difficult, so we use the AC as the point of force application.

Collecting moments

One can evaluate the moments anywhere using this model and they should equal zero for trim. They will be evaluated at the wing AC and the aircraft CG.

First, at the AC:

\[\Sigma M_{ac} = M_0 + W\left(h-h_0\right)\bar{c} - L_t\cdot\bar{l}_t\]

with the equilibrium steady flight condition this becomes

\[\Sigma M_{ac} = M_0 + L\left(h-h_0\right)\bar{c} - L_t\cdot\bar{l}_t\]

since

\[C_m=\frac{M}{\frac{1}{2}\rho V^2S\bar{c}}\]

then

\[C_{m_{ac}} = C_{m_0} + C_{L}\left(h-h_0\right)-C_{L_t}\eta_t\frac{S_t\,\bar{l}_t}{S_W\,\bar{c}}\]

where \(\eta_t=\frac{q_t}{q}\) and represents the loss in total head from the freestream to the tail.

Similarly the moments can be evaluated at the centre of gravity:

\[\Sigma M_{cg} = M_0 + L_w\left(h-h_0\right)\bar{c} - L_t\cdot l_t\]

and in coefficient form

\[C_{m_{cg}} = C_{m_0} + C_{L_w}\left(h-h_0\right)-C_{L_t}\eta_t\frac{S_t\,l_t}{S_W\,\bar{c}}\]

Two dimensionless parameters appear in the above expressions as the modified tail volume coefficient and tail volume coefficient, respectively:

\[\bar{V_H} = \frac{S_t}{S_W}\cdot\frac{\bar{l}_t}{\bar{c}}\]

\[V_H = \frac{S_t}{S_W}\cdot\frac{l_t}{\bar{c}}\]

giving

\[C_{m_{ac}} = C_{m_0} + C_{L}\left(h-h_0\right)-C_{L_t}\eta_t\,\bar{V_H}\]

\[C_{m_{cg}} = C_{m_0} + C_{L_w}\left(h-h_0\right)-C_{L_t}\eta_t\,V_H\]

For the aircraft to be in trim, the total moment must be zero - so these can be rearranged to yield an expression for the lift that the tail must produce to give trim

\[ C_{L_T} = \frac{C_{m0} + C_L\left(h-h_0\right)}{ \eta_T\,\bar{V}_H} = \frac{C_{m0} + C_{L_W}\left(h-h_0\right)}{\eta_T\,{V}_H}\]

The quanity \((h-h_0)\) is how far the CG is aft of the AC, so the tail lift is clearly directly proportional to this quantity. In reality, this relationship is more useful the other way around - that is, the amount of lift that the tail can produce dictates the CG limits.

A model for tail lift

The tail lift is assumed to be a function of the angle of attack and the elevator deflection angle

\[C_{L_T} = a_{t}\alpha_t + a_{e}\delta_e\]

where \(a_t\) is the tail lift curve slope, and \(a_e\) is the rate of change of tail lift with elevator deflection angle.

The angle of attack at the tail will be different to that of the wing due to the tailplane incidence, and the fact that the wing sits in the downwash of the wing.

\[\alpha_t = \alpha + i_t- \epsilon\]

hence

\[C_{L_T} = a_{t}\left(\alpha + i_t- \epsilon\right) + a_{e}\delta_e\]

the downwash at the tail is a function of the main wing bound vortex strength, and hence of the angle of attack

\[C_{L_T} = a_{t}\left(i_t + \alpha\left\{1-\frac{\partial\epsilon}{\partial\alpha}\right\}\right) + a_{e}\delta_e\]

\[C_{L_T} = a_{t}\left(i_t + \alpha\left\{1-\epsilon_\alpha\right\}\right) + a_{e}\delta_e\]

The expression above can be substituted into the two expressions for the pitching moment coefficient

\[C_{m_{ac}} = C_{m_0} + C_{L}\left(h-h_0\right)-\left[a_{t}\left(i_t + \alpha\left\{1-\epsilon_\alpha\right\}\right) + a_{e}\delta_e\right]\eta_t\,\bar{V_H}\]

\[C_{m_{cg}} = C_{m_0} + C_{L_w}\left(h-h_0\right)-\left[a_{t}\left(i_t + \alpha\left\{1-\epsilon_\alpha\right\}\right) + a_{e}\delta_e\right]\eta_t\,V_H\]

Downwash angle?

The derivative \(\epsilon_\alpha=\frac{\partial\epsilon}{\partial\alpha}\) is the rate of change of downwash angle with wing angle of attack. A detailed consideration of this effect is beyond the scope of this course, but you should be able to intuit the qualitative relatioship:

• The downwash will be larger with more lift, so \(\epsilon_\alpha\) must be positive for an aft tail

• \(\epsilon_\alpha\) should be inversely proportional to the vertical and horizontal separation of the wing and tail

• \(\epsilon_\alpha\) will increase with sweepback

• \(\epsilon_\alpha\) will decrease with aspect ratio

A detailed discussion of a potential solution to \(\epsilon_\alpha\) is provided in MacCormick:cite:`MacCormick:1995wq`, pg 486. I may include the potential model in this section as an interactive script at a future date…remind me if I haven’t.

For our purposes, an approximation will suffice. For an aircraft with an elliptical lift distribution, if it is assumed that the tail is ‘far’ downstream of the wing, then the induced angle of attack at the tail is reduced by twice the induced angle of attack at the wing. That is

\[\epsilon=-\delta\alpha_t=2\alpha_w\]

which, from lifting line theory is

\[\epsilon=\frac{2\cdot C_L}{\pi\cdot AR}\]

\[\epsilon_\alpha= \frac{4}{AR}\]

Elevator angle to trim

The equations derived are useful in that they can be set to zero and rearranged for the elevator deflection or the lift coefficient. This gives either the elevator deflection as a function of \(C_L\) or vice versa. This then enables determintion of the elevator angle required to reach certain speeds, or the speeds achievable with given elevator deflection angles.

Seeting \(C_{m_{ac}}=0\) and rearranging for \(\delta_e\) yields

(13)\[\delta_e=\frac{1}{a_e\,\eta_T\,\bar{V}_T}\left[C_{m_0} - C_L\left\{\frac{a_t}{a}\left[1-\epsilon_\alpha\right]\,\eta_t\,\bar{V}_t -(h-h_0)\right\}-a_t\,\eta_t\,\bar{V}_T\left\{i_t-\frac{C_{L_0}}{a}\left[1-\epsilon_\alpha\right]\right\} \right]\]

The expression above can be sense checked to prove that it shows sensible relationships based on what we know about aircraft:

Sign convention

The sign convention is not consistent for control surface deflectons from book to book, and often depends on different airframers. In my previous life doing stability and control transonic wind tunnel testing for different manufacturers, this could lead to confusing moments.

C’mon, that’s an amazing pun.

1. From the model developed, the sign convention is that elevator deflection is positive trailing edge down.

2. The equation above shows that the elevator angle is a linear, inverse function of \(C_L\). This is actually just due to the way that I’ve written it since the sign of \(\left\{\frac{a_t}{a}\left[1-\epsilon_\alpha\right]\,\eta_t\,\bar{V}_t -(h-h_0)\right\}\) is ambiguous at first glance. Generally, though, the left hand side terms will be greater than the right hand ones. So, \(\delta_e\propto-C_L\)

   This makes sense as we’d expect the elevator angle to become more negative with an increase in \(C_L\). If this doesn’t make sense to you, then consider that an increase on \(C_L\) is caused by an increase in \(\alpha\) hence requiring a nose up moment - hence, a reduction in lift on the tail.

3. It further shows that the elevator angle is a linear and positive function of the quantity \((h-h_0)\). Recall that this represents the CG position aft of the wing AC. Hence, with an aft CG, more elevator deflection is required.

Try and do this rearrangement yourself

It’s a bit of a bastard of algebra - and you’ll ned \(C_L=C_{L_0}+\alpha\cdot a\) to make it work.

It is also common to wish to have zero elevator deflection at the cruise condition.

Why do we wish to have \(\delta_e=0\) at cruise?

Elevator deflection increases the drag.

Setting the elevator deflection to zero allows for solution of either \(\bar{V}_H\) for a given \(i_t\) OR solution of \(i_t\) for a given \(\bar{V}_H\).

Relationship between lift coefficients, lift curve slopes

Quantities with a subscript \(()_w\) denote wing quantities, and \(()_t\) denote tail quantities. The dimensional lift is the sum of wing and lift

\[L=L_w + L_t\]

but

\[C_L\neq C_{L_w} + C_{L_t}\]

because of the different denominators in the two coefficients. Rather,

\[C_L= C_{L_w} + \eta_t\frac{S_t}{S}C_{L_t}\]

using the tail lift model:

\[C_L= C_{L_w} + \eta_t\frac{S_t}{S}\left[a_{t}\left(i_t + \alpha\left(1-\epsilon_\alpha\right)\right) + a_{e}\delta_e\right]\]

hence the total aircraft lift curve slope can now be denoted - for the stick-fixed case.

Stick Fixed meaning no input, since for steady flight, \(\delta_e\) is a function of \(\alpha\) and that’d be a much more complicated derivative to solve. Furthermore, we’re after the response of the aircraft withut any changes to controls.

\[a=\frac{\partial C_L}{\partial\alpha} = a_w + \eta_t\frac{S_t}{S}a_t\left(1-\epsilon_\alpha\right) \]

Stick Fixed Static Stability

With no control input, we will use the expression for \(C_{m_{ac}}\) and differentiate wrt \(\alpha\) to get \(C_{m_\alpha}\) thus yielding the stability criteria - since we know that \(C_{m_\alpha}<0\) for stability.

\[\frac{\partial C_{m_{ac}}}{\partial\alpha} = a\left(h-h_0\right) - \bar{V}_H\cdot\eta_t\cdot a_t\left(1-\epsilon_\alpha\right)\]

It is more common to work in terms of \(C_L\) rather than \(\alpha\) so

\[\frac{\partial C_m}{\partial C_L}=\frac{\partial C_m}{\partial \alpha}\frac{\partial \alpha}{\partial C_L}=\frac{\partial C_m}{\partial \alpha}\frac{1}{a}\]

\[\begin{split}\frac{\partial C_m}{\partial C_L}=\underbrace{\left(h-h_0\right)}_{\substack{\text{Distance between CG}\\ \text{and wing AC}}} - \underbrace{\bar{V}_H\cdot\eta_t\cdot\frac{a_t}{a}\left(1-\epsilon_\alpha\right)}_{\substack{\text{Horizontal Tail}\\ \text{Parameters}}}\end{split}\]

Since \(\frac{\partial C_m}{\partial C_L}\) will have the same sign as \(\frac{\partial C_m}{\partial\alpha}\), the stability criteria are the same. The boundary between positive and negative stability is governed by the above equation equallying zero.

Neutral Point

This defines the neutral point, which is the centre of gravity position that provides neutral stability. This is the most aft the CG can be before instability occurs (although flight with \(h=h_0\) is clearly not safe, either).

The neutral point has the symbol \(h_n\) and it can be shown:

\[\begin{split}h_n = \underbrace{h_0}_{\substack{\text{Wing AC}}} + \underbrace{\bar{V}_H\cdot\eta_t\cdot\frac{a_t}{a}\left(1-\epsilon_\alpha\right)}_{\substack{\text{Horizontal Tail}\\ \text{Parameters}}}\end{split}\]

Therefore, without the tail, the neutral point is the wing AC. The horizontal tail “pulls” the neutral point aft of this position

Static Margin

It follows from the above that the distance between the centre of gravity position and the neutral point dictates the degree of stability. This non-dimensional quantity is termed the static margin, \(H_n\)

Nondimensional?

Recall that \(h\) is the longitudinal CG location, nondimensionalised by MAC

\[H_n = h_n - h\]

Substituting \(h_n\) into the above yields

\[\begin{split}\begin{align} H_n &= h_0 - h + \eta_t\bar{V}_H\frac{a_t}{a}\left(1-\epsilon_\alpha\right)\\ &= -\frac{\partial C_m}{\partial C_L}\end{align}\end{split}\]

Since we need \(\frac{\partial C_m}{\partial\alpha}<0\) and hence \(\frac{\partial C_m}{\partial C_L}<0\), it can be observed that the static margin IS the pitch stiffness (well, it’s proportional to the pitch stiffness since \(C_{m_\alpha}\) is the actual stiffness) of the aircraft, and hence dictates the stability and how difficult it is to pitch the aircraft.

The aircraft becomes more difficult to pitch with an increase in static margin, and this can be shown.

Elevator lift coefficient gradient

Taking the elevator angle to trim, (13), and differentiating with respect to lift coefficient yields

\[\begin{split}\begin{align} \frac{\partial\delta_e}{\partial C_L} &= -\frac{1}{a_e\,\eta_t\,\bar{V}_H}\left[\frac{a_t}{a}\left(1-\epsilon_\alpha\right)\eta_t\bar{V}_H-\left(h-h_0\right)\right]\\ &= -\frac{1}{a_e\,\eta_t\,\bar{V}_H}H_n\end{align}\end{split}\]

again showing that a more stable aircraft is harder to change cruise speed.

Determination of NP by flight test

To determine/confirm the Neutral Point of an aircraft using flight test, a series of flights are performed with the longitudinal CG position varied (but still with the CG ahead of the predicted neutral point - else flight would occur with neutral stability, which is dangerous. During these flights, cruise trim is reached at a range of different lift coefficients to provide data such as the following, whereby the slope of \(\frac{\partial\delta_e}{\partial C_L}\) may be determined.

Fig. 35 Flight test data (obviously simulated) for elevator deflection angle for three CG locations

The gradient of a straight line through the data is proportional to \(C_{M_\alpha}\), so the stability boundary is the case with \(h=h_n\). The gradient can be plotted against the CG location, and a line fitted through these data: