Range and endurance have been mentioned in the preceding sections - and we have introduced that for maximum range the pilot should fly at \(V_{md}\), whilst to fly for maximum endurance the pilot should fly at \(V_{mp}\).
However - the above speeds are valid only for unpowered flight. So these speeds are suitable for a glider, but once an engine is introduced to an aircraft, these speeds no longer give the maximum range or the maximum endurance.
Furthermore, the propulsor type changes the speeds for both. In the following section, the best range and endurance speeds for jet and propeller-driven aircraft will be explored.
Range and Endurance#
Range and endurance are intuitive concepts:
Range (\(R\)): The maximum horizontal distance that an aircraft can cover.
Endurance (\(E\)): The time an aircraft can remain in flight
In the following analysis, the range and endurance for certain fuel quantities will be determined. For (hopefully) obvious reasons, some further definitions of range will help us here
Range subdefinitions#
Safe Range: The maximum distance between two airfields, for which an aircraft can fly a safe a reliable mission with a given payload.
This is an involved calculation involving take-off/landing/weather/diversion allowances etc. - there isn’t an easy means to do this calculation, so tends to be performed computationally.
For aircraft performance there are some more simple definitions of range:
Still Air Range (SAR): The maximum distance possible if an aircraft takes off, climbs to cruise altitude, and then cruises until all fuel is expended.
Obviously not desirable to run out of fuel at altitude, but SAR gives a good indication of the influence of aircraft parameters on range.
Gross Still Air Range (GSAR): The maximum distance possible if an aircraft commences cruise at altitude and continues until all fuel is expended.
The relationship between SAR and GSAR tends to be easy to define.
GSAR much easier to calculate
What will be covered here
Defining the problem#
To calculate GSAR, you might think that we need to:
find out the fuel flow rate, \(\dot{m}_{fuel}\) for thrust/power associated with \(V_{md}\)
get the endurance from the fuel mass, \(m_{fuel}\) divided by the flow rate \(E=\frac{m_{fuel}}{\dot{m}_{fuel}}\)
hence \(R=E\cdot V\)
The above reasoning is effectively how range is determined, but there are some complications that you may/may not be considering:
Aircraft take-off with a lot of fuel, so the aircraft weight changes with time and accordingly so do almost all the parameters we have considered up to this point, including the aircraft speed whilst the above relationship only holds true for constant airspeed
This means that some trade-offs have to be made in efficiency to allow a reasonable cruise - and we will see these
Breguet Range Equation#
The Breguet Range Equation (BRE) is named after a French aircraft designer, but was actually derived in the 1920’s by J G Coffin.
History and namesakes…
I’ve loosely read the history of the BRE and it being Coffin who actually came up with it in NACA Report 1969, but I’ve never actually delved into the legacy of this equation. If you wish to, and suggest a correct here, feel free.
The BRE allows a simple means to calculate GSAR, and can be defined in words as:
The BRE was first implemented for propeller aircraft, and is derived differently for thrust and power engines. In the following it will be derived separately for the two engines types.
Engine fuel burn#
To calculate the engine fuel burn of both types of engine, two new parameters are introduced
A parameter, \(c_t\), is introduced which is:
Thrust Specific Fuel Consumption (TSFC) for a turbojet \(c_t\) - mass of fuel burned per unit of thrust per second
Specific Fuel Consumption (SFC) for a turboprop \(c\) - mass of fuel burned per unit of power per second
Thrust specific fuel consumption - units#
In the above, the SI units are \(\left\{c_t\right\}=\left\{\frac{kg}{N\cdot s}\right\}\) which has dimensions of \(\left[\frac{\text{L}}{\text{T}}\right]\). You might see this expressed as \(\frac{g}{kN\,s}\), which is actually the same units.
In US customary units, this is \(\left\{c_t\right\}=\left\{\frac{lb}{lbf\cdot s}\right\}\).
You may see some slightly different units such as \(\left[\frac{kg}{kN\cdot hr}\right]\) so be sure to convert to SI or US customary base units
Specific fuel consumption - units#
In the above, the SI units are \(\left\{c\right\}=\left\{\frac{kg}{W\cdot s}\right\}\) which has dimensions of \(\left[\frac{\text{T}^2}{\text{L}^2}\right]\). You might see this expressed as \(\frac{g}{kW\,s}\), which is actually the same units.
In US customary units, this is \(\left\{c_t\right\}=\left\{\frac{lb}{hp\cdot s}\right\}\).
You may see some slightly different units such as \(\left[\frac{kg}{kW\cdot hr}\right]\) so be sure to convert to SI or US customary base units
The analysis is slightly different for jet and propeller-driven aircraft, so jet aircraft will be explored first.
BRE - Jet Aircraft#
The fundamental concept is, again:
So for a jet aircraft this is
which can be rearranged for the time
since the endurance/range is defined by cruise conditions, the equilibrium steady flight conditions of \(T=D\) and \(L=W\) can be utilised such that
which can be substituted into the BRE to give
for constant lift-to-drag ratio and TSFC, the equation above can be integrated with the limits \(t_{0}\) and \(t_{1}\) corresponding to \(W_{0}\) and \(W_{1}\) where 0 denotes the start of cruise, and 1 denotes the end.
This yields the endurance, \(E\):
Jet Aircraft: Maximum Endurance#
For a given \(c_t\), \(W_0\), and \(W_{1}\), Equation (8) shows that the best endurance for a jet aircraft is found at the minimum drag speed. If you’re unsure why it shows this - look at the equation and consider what can be maximised.
To find the range, we’ll take a step back to the Equation (7) and substitute the aircraft speed equation.
Jet Aircraft: Range#
Taking Equation{eq} ACSpeedEquation and multiplying Equation (7) by it yields the incremental distance, \(dS\), covered during cruise
Don’t be tempted to combine the two \(W\) terms at this point - those will be dealt with in a little while, first some observations can be made about the equation above:
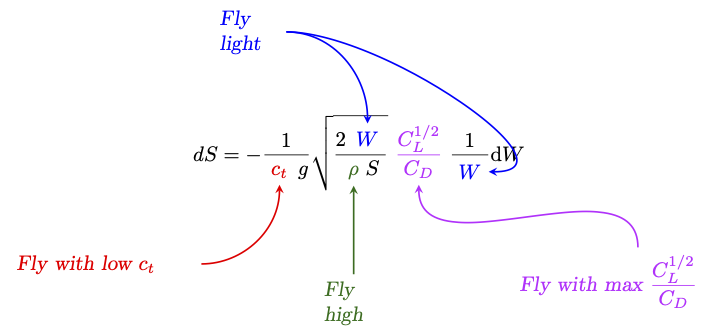
As with all things in aeronautics (well, with science and mathematics), if you derive a relationship, you should check that what it says makes sense. The equation above says:
Range is inversely proportional to fuel burn, which makes sense
Range is inversely proportonal to weight, which makes sense (combine the two into \(W^{-1/2}\))
Range is proportional to altitude (we know aircraft cruise at altitude)
We see that the best range is given at the aerodynamic condition (that is, the velocity) corresponding to the maximum value of \(\frac{C_L^{1/2}}{C_D}\) which is given by:
For equilibrium, lift must equal weight, so for the best \(C_L\), this occurs at a single airspeed (Eq. (5)
Fuel is burned, so the aircraft gets lighter, so looking at the definition of the lift coefficient:
To maintain the best \(C_L\), either the velocity has to reduce or the density has to reduce.
This yields two types of cruise:
Constant Velocity aka Cruise-Climb
Constant Altitude (where the aircraft slows down)
Constant Velocity Cruise#
Looking at the definition of the lift coefficient, if velocity is constant, then in order to maintain a constant \(C_L=\sqrt{\frac{C_{D0}}{3\,K}}\), the ratio \(\frac{W}{\rho}\) must be constant. Accordingly, whilst the terms \(W\) and \(\rho\) both change during the cruise and could be included in the integration, the ratio of them is a constant, and can be removed from the integration. If the aircraft starts at an altitude \(h_0\) with a corresponding density \(\rho_0\), then
where \(n\) is any intermediate value between the start and end of the cruise. Hence \(\frac{W}{\rho}\) can be replaced with \(\frac{W_0}{\rho_0}\). That is
You should be able to see that the range is a function of the starting altitude (to which \(\rho_0\) corresponds) - that is, if a cruise is commenced at a higher altitude, the range will be greater.
To determine the end altitude, this can be simply yielded from the relationship between weight and density.
Constant Altitude Cruise#
Conversely, if the altitude is held constant, then the ratio of
must be held constant. But since there is no such ratio in the expression for incremental distance, the weight must be moved into the integral:
Similarly, the variation of velocity can be yielded from the aircraft weight to velocity ratio.
Jet BRE: Numerical Example#
About units
You (that’s you, IIT student) should be able to do these calculations both in SI units and US customary units. Since I got my degree and PhD outside of America, I have an appreciation (to use the term loosely) for US customary units, but my actual application has always been to convert to SI at the start, and then convert the answer back to US customary units if I need to provide one.
For this reason, I work in SI in written examples for class but I will provide examples with US customary units used throughout. I simply don’t want to make a mistake when going through work in class, and end up a factor of 32 out, or have mixed up lb for lbf or whatever else I could have done.
I managed to find this whilst googling about the US and the metric system, if you want some further reading. https://www.nist.gov/system/files/documents/pml/wmd/metric/1136a.pdf
This is an adaptation of Example 5.19 in Anderson - I claim no originality or authorship for the data provided, but I’ve used it to confirm my US customary calculation is correct before adapting.
Question:
Estimate the maximum range at altitudes of 20,000, 30,000, and 40,000 feet for the Gulfstream IV given the following:
Mass of aircraft without fuel: 43,500lb. Mass of usable fuel: 29,500lb. Drag model: \(C_D=0.015 + 0.08\cdot C_L^2\) Wing area: 950 square feet TSFC: 0.69 lb of fuel consumed per pound of thrust per hour.
Compare the constant altitude, and the cruise-climb (constant speed ranges).
Show the starting/ending speeds and altitudes for the respective cruise methods.
Show code cell source
import numpy as np
from ambiance import Atmosphere
h1 = 20000
h2 = 30000
h3 = 40000
m_1 = 43500 # mass in lbs of aircraft without fuel
m_fuel = 29500 # mass in lbs of fuel
# # Unit conversions
lb_to_kilo = 0.453592
pound_to_newton = 4.44822
hour_to_second = 3600
ft_to_metre = 0.3048
metre_to_miles = 0.000621371
km_to_miles = 0.621371
g = 9.80665 # Gravitational acceleration
kg_to_slugs = 0.0685218
miles_to_feet = 5280 # Because everyone recalls this number...
ms_to_knots = 1.94384
# The start weight of the aircraft is equal to the end weight plus the fuel weight
m_0 = m_1 + m_fuel
# Aircraft drag model - from Anderson
CD0 = 0.015
K = 0.08
S = 950 # In square feet
# Thrust specific fuel consumption
c_t = 0.69 # c_t in lb of fuel per pound of thrust per hour
# Convert c_t to consistent units (lb of fuel per pound of thrust per second, not per hour)
c_t = c_t / 3600
# Find the Cl and Cd for max range
Cl = np.sqrt(CD0/3/K)
Cd = CD0 + K * Cl**2
V = np.zeros(3)
# Make an interpolant for the altitude based on the density:
from scipy.interpolate import interp1d
altitudes = np.linspace(0, 80e3, 10000)
densities = Atmosphere(altitudes).density
altdens = interp1d(densities, altitudes, kind='cubic')
# Iterate over the altitudes
for i, h_ft in enumerate([h1, h2, h3]):
############################################################################
################### First do the calculation in US customary units
############################################################################
# Get density for this altitude - this will be in SI
h = h_ft * ft_to_metre
Atmopshere_for_altitude = Atmosphere(h)
rho_SI = Atmopshere_for_altitude.density[0]
print(f"For an altitude of {h_ft:1.0f}ft/{h/1e3:1.1f}km")
# Convert to US customary density units of slugs per cubic feet
rho_US = rho_SI * kg_to_slugs * ft_to_metre**3 # i.e., dividing be the reciprocal of ft_to_metre**3
# Now get range - which will be in feet (US Customary base units), so convert to miles for readability
## Note that since c_t has been defined as a mass, and so has the aircraft mass - we can avoid using "g" by
# keeping the aircraft mass as mass since "g" is in the denominator of the BRE
# If you don't want to do this you can save g in US customary as 32.17405ft/s^2, but the pounds/pounds/poundal
# conversion can be a real pain
# Constant altitude range
Range_constant_altitude = 1/c_t * np.sqrt(8/rho_US/S) * Cl**.5 / Cd * (m_0**.5 - m_1**.5) / miles_to_feet
# Constant speed range
Range_constant_speed = 1/c_t * np.sqrt(2*m_0/rho_US/S) * Cl**.5 / Cd * (np.log(m_0/m_1)) / miles_to_feet
print("US Customary Unit Calcs:")
print(f"The constant altitude range is {Range_constant_altitude:1.0f} miles")
print(f"The cruise-climb range is {Range_constant_speed:1.0f} miles")
############################################################################
################### Now in SI units
############################################################################
# Do the conversion into SI units
c_t_SI = c_t * lb_to_kilo / pound_to_newton
# Find the Cl and Cd for best range
Cl = np.sqrt(CD0/3/K)
Cd = CD0 + K * Cl**2
# wing area
S_SI = S * ft_to_metre**2
# Convert units
w_0 = m_0 * lb_to_kilo * g
w_1 = m_1 * lb_to_kilo * g
# Determine constant altitude range in km
Range_constant_altitude = 1/c_t_SI / g * np.sqrt(8/rho_SI/S_SI) * Cl**.5 / Cd * (w_0**.5 - w_1**.5) / 1e3
# Determine constant speed range in km
Range_constant_speed = 1/c_t_SI / g * np.sqrt(2*w_0/rho_SI/S_SI) * Cl**.5 / Cd * (np.log(w_0/w_1)) / 1e3
print(" ")
print("SI Unit Calcs:")
print(f"The constant altitude range is {Range_constant_altitude:1.0f}km which is equal to {Range_constant_altitude*km_to_miles:1.0f} miles")
print(f"The cruise-climb range is {Range_constant_speed:1.0f}km which is equal to {Range_constant_speed*km_to_miles:1.0f} miles")
print(" ")
# Determine the speed difference for the constant altitude cruise
v0 = np.sqrt(w_0 / (0.5 * rho_SI * S_SI * Cl)) * ms_to_knots
v1 = np.sqrt(w_1 / (0.5 * rho_SI * S_SI * Cl)) * ms_to_knots
# Determine the altitude difference for cruise climb
rho_1 = 2*w_1/S_SI/Cl/(v0/ms_to_knots)**2
h_1 = altdens(rho_1)/ft_to_metre
print(f"For the constant altitude cruise, the starting speed is {v0:1.0f}knTAS and the end speed is {v1:1.0f}knTAS")
print(f"For the cruise-climb the aircraft gains {(h_1 - h_ft)/1e3:1.1f} thousand feet during the cruise")
print(" ")
print("-------------------------------------------------------------- ")
print(" ")
For an altitude of 20000ft/6.1km
US Customary Unit Calcs:
The constant altitude range is 3924 miles
The cruise-climb range is 4454 miles
SI Unit Calcs:
The constant altitude range is 6315km which is equal to 3924 miles
The cruise-climb range is 7167km which is equal to 4454 miles
For the constant altitude cruise, the starting speed is 413knTAS and the end speed is 319knTAS
For the cruise-climb the aircraft gains 14.4 thousand feet during the cruise
--------------------------------------------------------------
For an altitude of 30000ft/9.1km
US Customary Unit Calcs:
The constant altitude range is 4680 miles
The cruise-climb range is 5312 miles
SI Unit Calcs:
The constant altitude range is 7533km which is equal to 4680 miles
The cruise-climb range is 8549km which is equal to 5312 miles
For the constant altitude cruise, the starting speed is 492knTAS and the end speed is 380knTAS
For the cruise-climb the aircraft gains 12.1 thousand feet during the cruise
--------------------------------------------------------------
For an altitude of 40000ft/12.2km
US Customary Unit Calcs:
The constant altitude range is 5764 miles
The cruise-climb range is 6542 miles
SI Unit Calcs:
The constant altitude range is 9276km which is equal to 5764 miles
The cruise-climb range is 10529km which is equal to 6542 miles
For the constant altitude cruise, the starting speed is 606knTAS and the end speed is 468knTAS
For the cruise-climb the aircraft gains 10.8 thousand feet during the cruise
--------------------------------------------------------------
Variation of jet range with lift coefficient, airspeed#
Recall that the lift coefficient is effectively a measure of the aircraft cruise speed. The range can be plotted vs. lift coefficient and forward speed for the two different jet cruise cases over a range of starting altitudes.
You can click on the entries in the legend to hide/show different plots.
Beware of source for the plots below…
Producing the plots below is fairly simple - but in order to get the labels and legend to work correctly, there’s a bit of obscure logic flow in the way the plot is created.
That is, it makes it look more complicated than it actually is (and it probably could be done better if I knew my way around plotly better).
Show code cell source
import numpy as np
import plotly.graph_objects as go
import plotly.express as px
plotcols = px.colors.qualitative.Plotly
## Note that there's a lot of slightly peculiar logic in the code below that enables the annotation and the legend
# to to be printed. You don't need to worry about it.
# Aircraft drag model - from Anderson
CD0 = 0.015
K = 0.08
S = 950 # In square feet
S = S * ft_to_metre**2
rho_sl = 1.2255
# Define a range of Cls
CLrange = np.linspace(.1, 1.2, 1000)
# Drag is given from the drag model
CDrange = CD0 + K * CLrange**2
# The CL and CD for TRCC and TUCC are defined above, so they can be reused here
# Open three figures
fig = go.Figure()
fig2 = go.Figure()
fig3 = go.Figure()
# Make sigma function for convenience
def sigma_function(alt):
mosphere = Atmosphere(alt)
rho = mosphere.density[0]
sig = rho/rho_sl
return sig
# Iterate over altitudes
for i, h in enumerate(np.arange(4, 14, 2)*1e3):
# Get the density ratio
sig = sigma_function(h)
# Determine the cruise speed in TAS at this altitude
Vtas_knots = np.sqrt(w_0 / (.5 * sig * rho_sl * S * CLrange)) /.5144444
Veas_knots = np.sqrt(w_0 / (.5 * rho_sl * S * CLrange)) /.5144444
######## Get the two speeds
Range_constant_speed = 1/c_t_SI/g * np.sqrt(2*w_0/rho_sl/sig/S_SI) * CLrange**.5 / CDrange * (np.log(w_0/w_1)) / 1e3
Range_constant_altitude = 1/c_t_SI/g * np.sqrt(8/rho_sl/sig/S_SI) * CLrange**.5 / CDrange * (w_0**.5 - w_1**.5) / 1e3
# Plot it
if i == 0:
fig.add_trace(go.Scatter(x=CLrange, y=Range_constant_speed, legendgroup = "Constant Speed", mode="lines", name=f"Constant Speed - {h/1e3:1.0f}km", line=dict(width=4,
dash='dash', color=plotcols[i])))
fig2.add_trace(go.Scatter(x=Veas_knots, y=Range_constant_speed, legendgroup = "Constant Speed", mode="lines", name=f"Constant Speed - {h/1e3:1.0f}km", line=dict(width=4,
dash='dash', color=plotcols[i])))
fig3.add_trace(go.Scatter(x=Vtas_knots, y=Range_constant_speed, legendgroup = "Constant Speed", mode="lines", name=f"Constant Speed - {h/1e3:1.0f}km", line=dict(width=4,
dash='dash', color=plotcols[i])))
else:
fig.add_trace(go.Scatter(x=CLrange, y=Range_constant_speed, legendgroup = "Constant Speed", mode="lines", showlegend=True, name=f"Constant Speed - {h/1e3:1.0f}km", line=dict(width=4,
dash='dash', color=plotcols[i])))
fig2.add_trace(go.Scatter(x=Veas_knots, y=Range_constant_speed, legendgroup = "Constant Speed", mode="lines", showlegend=True, name=f"Constant Speed - {h/1e3:1.0f}km", line=dict(width=4,
dash='dash', color=plotcols[i])))
fig3.add_trace(go.Scatter(x=Vtas_knots, y=Range_constant_speed, legendgroup = "Constant Speed", mode="lines", showlegend=True, name=f"Constant Speed - {h/1e3:1.0f}km", line=dict(width=4,
dash='dash', color=plotcols[i])))
# Plot it
if i == 0:
fig.add_trace(go.Scatter(x=CLrange, y=Range_constant_altitude, legendgroup = "Constant Altitude", mode="lines", name=f"Constant Altitude - {h/1e3:1.0f}km", line=dict(width=4, color=plotcols[i])))
fig2.add_trace(go.Scatter(x=Veas_knots, y=Range_constant_altitude, mode="lines", legendgroup = "Constant Altitude", name=f"Constant Altitude - {h/1e3:1.0f}km", line=dict(width=4, color=plotcols[i])))
fig3.add_trace(go.Scatter(x=Vtas_knots, y=Range_constant_altitude, mode="lines", legendgroup = "Constant Altitude", name=f"Constant Altitude - {h/1e3:1.0f}km", line=dict(width=4, color=plotcols[i])))
else:
fig.add_trace(go.Scatter(x=CLrange, y=Range_constant_altitude, mode="lines", legendgroup = "Constant Altitude", name=f"Constant Altitude - {h/1e3:1.0f}km", showlegend=True, line=dict(width=4, color=plotcols[i])))
fig2.add_trace(go.Scatter(x=Veas_knots, y=Range_constant_altitude, mode="lines", legendgroup = "Constant Altitude", name=f"Constant Altitude - {h/1e3:1.0f}km", showlegend=True, line=dict(width=4, color=plotcols[i])))
fig3.add_trace(go.Scatter(x=Vtas_knots, y=Range_constant_altitude, mode="lines", legendgroup = "Constant Altitude", name=f"Constant Altitude - {h/1e3:1.0f}km", showlegend=True, line=dict(width=4, color=plotcols[i])))
# ####### Label the altitudes:
# if i == 0: fig.add_trace(go.Scatter(x=[CLrange[0]], y=[R_trcc[0]], mode="text", text="All altitudes", textposition="middle right", name="Annotation"))
# fig.add_trace(go.Scatter(x=[CLrange[0]], y=[R_tucc[0]], mode="text", text=f"{h/1e3:1.0f}km", textposition="middle left", showlegend=False))
# if i == 0: fig2.add_trace(go.Scatter(x=[Veas_knots[0]+16*i + 2], y=[R_trcc[0]], mode="text", text="All altitudes", textposition="middle right", name="Annotation"))
# fig2.add_trace(go.Scatter(x=[Veas_knots[0]+2], y=[R_tucc[0]], mode="text", text=f"{h/1e3:1.0f}km", textposition="middle right", name="Annotation"))
# fig3.add_trace(go.Scatter(x=[Vtas_knots[0]], y=[R_tucc[0]], mode="text", text=f"{h/1e3:1.0f}km", textposition="bottom center", name="Annotation"))
# fig3.add_trace(go.Scatter(x=[Vtas_knots[0]], y=[R_trcc[0]], mode="text", text=f"{h/1e3:1.0f}km", textposition="bottom center", name="Annotation"))
# Determine the different Cls to plot for comparison
CL_mr = np.sqrt(CD0/3/K)
CL_md = np.sqrt(CD0/K)
CL_mp = np.sqrt(3*CD0/K)
# Overlay lines for different Cls on the first figure only
fig.add_trace(go.Scatter(x=[CL_mr, CL_mr], y=[3000, 12000], showlegend=False, mode="lines", line=dict(color="darkgreen")))
fig.add_trace(go.Scatter(x=[CL_md, CL_md], y=[3000, 12000], showlegend=False, mode="lines", line=dict(color="mediumpurple")))
fig.add_trace(go.Scatter(x=[CL_mp, CL_mp], y=[3000, 12000], showlegend=False, mode="lines", line=dict(color="crimson")))
fig.add_trace(go.Scatter(x=[CL_mr], y=[2000], mode="text",\
text="$C_{L,mr}=\sqrt{\\frac{C_{D0}}{3\,K}}$",\
textposition="bottom center", showlegend=False,\
textfont=dict(color="darkgreen")))
fig.add_trace(go.Scatter(x=[CL_md], y=[2000], mode="text",\
text="$C_{L,md}=\sqrt{\\frac{C_{D0}}{K}}$",\
textposition="bottom center", showlegend=False,\
textfont=dict(color="mediumpurple")))
fig.add_trace(go.Scatter(x=[CL_mp], y=[2000], mode="text",\
text="$C_{L,mp}=\sqrt{\\frac{3\,C_{D0}}{K}}$",\
textposition="bottom center", showlegend=False,\
textfont=dict(color="crimson")))
# Overlay lines for the EAS
def CLtoEAS(CL):
V = np.sqrt(w_0/(.5 * rho_sl * S * CL)) /.5144444
return V
fig2.add_trace(go.Scatter(x=[CLtoEAS(CL_mr), CLtoEAS(CL_mr)], y=[3000, 12000], showlegend=False, mode="lines", line=dict(color="darkgreen")))
fig2.add_trace(go.Scatter(x=[CLtoEAS(CL_md), CLtoEAS(CL_md)], y=[3000, 12000], showlegend=False, mode="lines", line=dict(color="mediumpurple")))
fig2.add_trace(go.Scatter(x=[CLtoEAS(CL_mp), CLtoEAS(CL_mp)], y=[3000, 12000], showlegend=False, mode="lines", line=dict(color="crimson")))
fig2.add_trace(go.Scatter(x=[CLtoEAS(CL_mr)], y=[2000], mode="text",\
text="$V_{C_{L,mr}}$",\
textposition="bottom center", showlegend=False,\
textfont=dict(color="darkgreen")))
fig2.add_trace(go.Scatter(x=[CLtoEAS(CL_md)], y=[2000], mode="text",\
text="$V_{C_{L,md}}$",\
textposition="bottom center", showlegend=False,\
textfont=dict(color="mediumpurple")))
fig2.add_trace(go.Scatter(x=[CLtoEAS(CL_mp)], y=[2000], mode="text",\
text="$V_{C_{L,mp}}$",\
textposition="bottom center", showlegend=False,\
textfont=dict(color="crimson")))
# Remove junk legend entries - this would be more efficient if I weren't lazy
for trace in fig['data']:
if (trace['name'] == "DontPrint") or (trace['name'] == "Annotation"): trace['showlegend'] = False
for trace in fig2['data']:
if (trace['name'] == "DontPrint") or (trace['name'] == "Annotation"): trace['showlegend'] = False
for trace in fig3['data']:
if (trace['name'] == "DontPrint") or (trace['name'] == "Annotation"): trace['showlegend'] = False
fig.update_layout(
title="Constant speed and constant altitude ranges vs. Lift Coefficient for different starting altitudes",
xaxis_title="$C_L$",
yaxis_title="Range/km",
)
fig2.update_layout(
title="Constant speed and constant altitude ranges vs. EAS for different starting altitudes",
xaxis_title="$V_{E}/\\text{kn}$",
yaxis_title="Range/km",
)
fig3.update_layout(
title="Constant speed and constant altitude ranges vs. TAS for different starting altitudes",
xaxis_title="$V/\\text{kn}$",
yaxis_title="Range/km",
)
# Figure 1
fig.update_xaxes(range=[0, 1.5])
fig.update_yaxes(range=[0, 12000])
fig2.update_yaxes(range=[0, 12000])
fig2.update_xaxes(range=[0, 500])
fig3.update_yaxes(range=[0, 12000])
fig.show()
fig2.show()
fig3.show()
<>:108: SyntaxWarning: invalid escape sequence '\s'
<>:112: SyntaxWarning: invalid escape sequence '\s'
<>:116: SyntaxWarning: invalid escape sequence '\s'
<>:108: SyntaxWarning: invalid escape sequence '\s'
<>:112: SyntaxWarning: invalid escape sequence '\s'
<>:116: SyntaxWarning: invalid escape sequence '\s'
/var/folders/4w/4bcfp26j6_1gn39czlk991z80000gn/T/ipykernel_85503/447768783.py:108: SyntaxWarning: invalid escape sequence '\s'
text="$C_{L,mr}=\sqrt{\\frac{C_{D0}}{3\,K}}$",\
/var/folders/4w/4bcfp26j6_1gn39czlk991z80000gn/T/ipykernel_85503/447768783.py:112: SyntaxWarning: invalid escape sequence '\s'
text="$C_{L,md}=\sqrt{\\frac{C_{D0}}{K}}$",\
/var/folders/4w/4bcfp26j6_1gn39czlk991z80000gn/T/ipykernel_85503/447768783.py:116: SyntaxWarning: invalid escape sequence '\s'
text="$C_{L,mp}=\sqrt{\\frac{3\,C_{D0}}{K}}$",\
Notice that the maximum range is found at a considerably higher speed than both the minimum power and minimum drag speeds, for both types of cruise climb. The ratio between the best range speed and the minimum drag speed may be readily shown.
These ratios hold across altitudes, as you should expect.
BRE - Propeller Aircraft#
The BRE for propeller aircraft is similar to that for jet aircraft, but SFC is used in place of TSFC - the SI units are \(\text{kg}/{\text W s}\).
The BRE for propeller aircraft is
where \(P\) is the power delivered to the aircraft from the propeller. With \(\eta\) as the propeller efficiency, the power delivered is function of the power required
so the BRE becomes
Assuming, as for the jet cruise-climb case, that \(\tfrac{C_L}{C_D}\), \(f\), and \(V\) remain constant, the equation above can be integrated from \(W_S\) to \(W_E\) to yield the endurance, \(E\):
Propeller Aircraft: Maximum Endurance#
Equation (11) shows that for the maximum endurance for a propeller-driven aircraft, the quanity \(\frac{C_L}{V\,C_D}\) must be maximised, which is different to the jet aircraft case.
Clearly the maximum endurance is found at the minimum power condition, thus for maximum endurance a propeller-driven aircraft should fly at \(V_{mp}\).
Propeller Aircraft: Maximum Range#
The increment in aircraft distance, \(\text{d}S\) when flown at velocity \(V\) is given by
Clearly the maximum endurance is found at the minimum drag condition, thus for maximum endurance a propeller-driven aircraft should fly at \(V_{md}\).
Hence the maximum range is given by the integration \(R=\int\text{d}S\)
Range and Endurance Summary#
| Glider | Jet Aircraft | Propeller Aircraft | |
|---|---|---|---|
| Maximum Endurance | At $V_{mp}$ | At $V_{md}$ | At $V_{mp}$ |
| Maximum Range | At $V_{md}$ | $\gt V_{md}$ | At $V_{md}$ |
All of the cruise-climb scenarios are theoretical behaviour, and are reliant on the assumptions made within these models - furthermore, cruise-climb is typically not allowed by ATC. Rather, a series of stepped-climbs are made.
Nonetheless, the methods shown here allow a good estimate of range to be made - and afford the ability to look at the effect of design parameters on range and endurance.
